Multiplicación por duplicación
es un antiguo algoritmo de multiplicación. No requiere conocer la tabla de
multiplicar, aunque se necesita saber sumar. En el método ruso, se requiere
además saber dividir entre 2.
Este método fue empleado con profusión en el Antiguo Egipto y conocido como
duplicación y mediación. Hoy en día el
método es utilizado por campesinos en países como Rusia. De hecho, en inglés
este método se conoce como el "método campesino ruso". Los dos
métodos son algo diferentes en la forma pero, obviamente, se llega al mismo
resultado.
En el Antiguo Egipto, el método utilizado sólo requiere saber sumar:
Si deseamos multiplicar
A x
B
- En la primera columna se escribe la serie:
 , partiendo desde
, partiendo desde 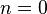 continuando mientras
continuando mientras  . Los primeros números de la serie quedarían de la siguiente manera: 1,2,4, 8...
. Los primeros números de la serie quedarían de la siguiente manera: 1,2,4, 8...
- En la segunda columna se escribe la serie:
 , o bien
, o bien  siendo
siendo  . El resultado es el mismo y obtendremos la siguiente serie:B, 2B, 4B...
. El resultado es el mismo y obtendremos la siguiente serie:B, 2B, 4B...
- En una tercera columna se marcan las cifras de la primera columna cuya suma resulte igual a A (de mayor a menor)
- El resultado es la suma de las cifras marcadas de la segunda columna.
Ejemplo: 41 × 59
1 59
______________
1 59 X
2 118
4 236
8 472 X
16 944
32 1888 X como (32 + 8 + 1 = 41)
______________
41 2419 el resultado será 1888 + 472 + 59 = 2419.


 , partiendo desde
, partiendo desde 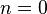 continuando mientras
continuando mientras  . Los primeros números de la serie quedarían de la siguiente manera: 1,2,4, 8...
. Los primeros números de la serie quedarían de la siguiente manera: 1,2,4, 8... , o bien
, o bien  siendo
siendo  . El resultado es el mismo y obtendremos la siguiente serie:B, 2B, 4B...
. El resultado es el mismo y obtendremos la siguiente serie:B, 2B, 4B...